KMP
1. KMP 算法介绍
KMP 算法:全称 「Knuth Morris Pratt 算法」,由 Donald Knuth、James H. Morris、Vaughan Pratt 在 1977 年联合发表。
KMP 算法思想:对于给定文本串 和模式串 ,当发现文本串的某个字符与模式串失配时,利用模式串的部分匹配信息尽量减少匹配次数,避免文本串的指针回退。
1.1 朴素匹配算法的缺陷
在朴素匹配算法中,分别用指针 和 表示文本串 和模式串 的当前匹配位置。当字符失配时:
- 回退到起始位置;
- 回退到匹配开始位置的下一个字符,重新进行匹配。
示例图展示了朴素匹配算法的过程(失配后重新尝试从下一字符开始匹配):
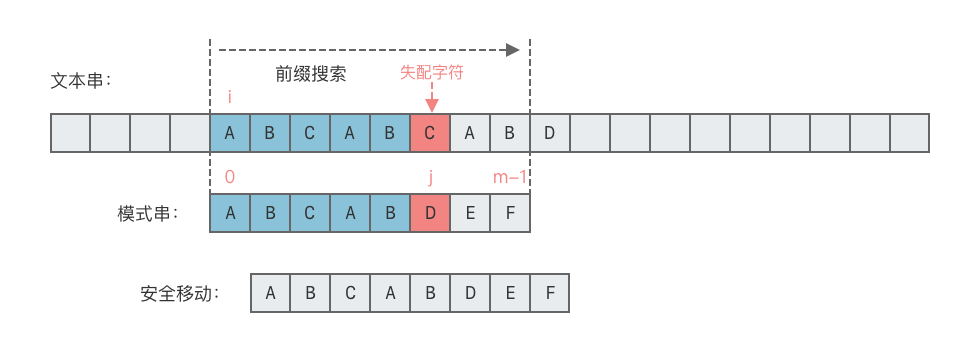
在这种情况下,如果匹配字符较多且发生多次失配,匹配效率会很低。
1.2 KMP 算法的改进
KMP 算法通过预处理模式串 ,构造一个 前缀表(lps 表),在匹配过程中借助前缀表的信息优化模式串指针的移动,使得主串指针 无需回退。
以示例为例:
- 模式串
P在匹配时,若在 处失配:- 已知 ;
- 根据前缀表信息,模式串的前缀和后缀存在部分相等,如下图蓝色部分表示:
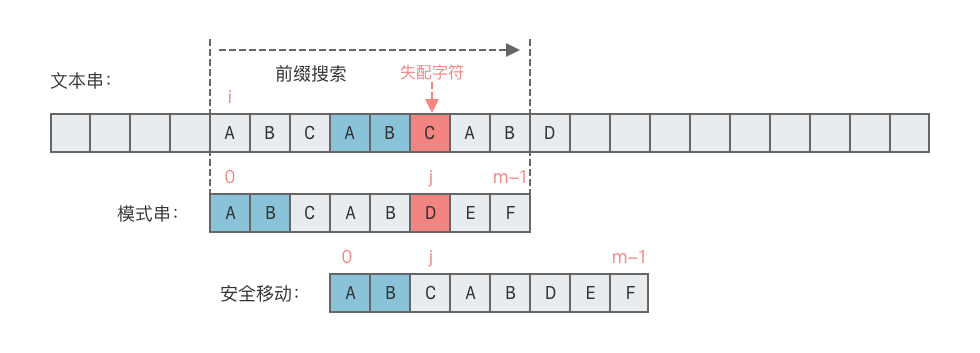
- 可直接将模式串指针 回退至前缀表中记录的位置(避免主串回退)。
2. KMP 算法的关键数据结构
2.1 前缀表(lps)
前缀表(lps 表,Longest Prefix Suffix)用于存储模式串的部分匹配信息。
- 定义:
lps[j]表示模式串 中以第 个字符结尾的子串 的最长相等前后缀的长度。
示例:P = "ABCABCD"
| 子串 | 前缀 | 后缀 | 最长相等前后缀长度 |
|---|---|---|---|
| A | - | - | 0 |
| AB | A | B | 0 |
| ABC | AB | BC | 0 |
| ABCA | A | A | 1 |
| ABCAB | AB | AB | 2 |
| ABCABC | ABC | ABC | 3 |
| ABCABCD | ABCA | BCD | 0 |
前缀表 lps 为:[0, 0, 0, 1, 2, 3, 0]。
3. KMP 算法步骤
3.1 前缀表(lps)的构造
构造 lps 表的逻辑如下:
- 初始化两个指针:
length:表示当前匹配的最长前缀长度;i:遍历模式串 的后缀位置(从索引 1 开始)。
- 如果
P[length] == P[i],更新lps[i] = length + 1并移动指针。 - 如果失配,
length回退到lps[length - 1]。 - 重复以上步骤直至模式串遍历完毕。
3.2 KMP 匹配过程
- 初始化两个指针:
i:指向文本串 的当前匹配位置;j:指向模式串 的当前匹配位置。
- 若
T[i] == P[j],同时移动i和j。 - 若失配,利用
lps表调整模式串位置:j = lps[j - 1]。 - 若
j == P.length,说明模式串完全匹配,返回匹配起始位置i - j + 1。 - 若文本串遍历完毕仍未匹配,返回
-1。
4. KMP 算法代码实现
Python 实现
1 | # 构造前缀表(lps 表) |
Java 实现
1 | class Solution { |
代码解析
1. 前缀表构造
- 方法:
generateLPS:- 使用双指针
i和length:i遍历模式串;length表示当前匹配的最长前缀长度。
- 如果匹配成功(
P[i] == P[length]),更新lps[i] = length + 1,并移动指针。 - 如果失配,根据前缀表回退:
length = lps[length - 1]。
- 使用双指针
2. 匹配过程
- 方法:
strStr:- 使用双指针
i和j:i遍历文本串;j遍历模式串。
- 匹配失败时,模式串指针
j回退:j = lps[j - 1]。 - 如果
j == m(模式串完全匹配),返回匹配的起始位置i - m + 1。
- 使用双指针
运行示例
运行代码后,输出结果:
1 | 0 |
5.时间复杂度分析
- 前缀表构造:,模式串长度为 。
- 匹配过程:,文本串长度为 。
- 总复杂度:。
KMP 算法的效率大大优于朴素匹配算法,特别是在长文本串和长模式串的情况下。
6.相关题目
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
Comments